Integrating const-generics to nalgebra 0.26
Today we released the version 0.26 of our general-purpose linear-algebra crate: nalgebra 🎊
The version 1.51.0 of Rust has been released three weeks ago. That version stabilized an MVP for one of the feature we wanted the most: const-generics. Const-generics allow you to define types parametrized by const integers, chars, or booleans. One iconic example is writing a structure wrapping an array of any size:
// Example taken from the 1.51 Rust announcement.
struct Array<T, const LENGTH: usize> {
list: [T; LENGTH]
}
nalgebra supports matrices (and vectors) with dimensions known at runtime or at compile-time.
The components of matrices/vectors with dimensions known at runtime are stored in a Vec<T>.
Before nalgebra 0.26, matrices/vectors with dimensions known at compile-time were stored
in a GenericArray, from the excellent generic-array
crate. Thanks to const-generics, we were able to replace GenericArray by standard arrays: [[T; R]; C]
(where R is the number of rows, and C the number of columns) in nalgebra 0.26.
This change results in significant ergonomics improvements when using statically-sized matrices or vectors:
1. Simpler generic programming with statically-sized entities
Using nalgebra for generic programming with statically-sized matrices/vectors/points was quite challenging before. Let's take a simple example of a generic structure that wraps a point, a vector, and a matrix and performs some kind integration using 64-bit precision. In previous version of nalgebra this would look like this:
use nalgebra::{DimName, MatrixMN, VectorN, Point, DefaultAllocator, allocator::Allocator};
struct Integrator<D: DimName>
where DefaultAllocator: Allocator<f32, D, D> + Allocator<f32, D> {
m: MatrixMN<f32, D, D>,
v: VectorN<f32, D>,
p: Point<f32, D>
}
impl<D: DimName> Integrator<D>
where DefaultAllocator: Allocator<f32, D, D> + Allocator<f32, D> {
// A method that performs some kind of integration
// using `f64` intermediate results.
pub fn integrate_highp(&self, dt: f32) -> Point<f32, D>
where
MatrixMN<f32, D, D>: Copy,
VectorN<f32, D>: Copy,
Point<f32, D>: Copy,
DefaultAllocator: Allocator<f64, D, D> + Allocator<f64, D> {
// First cast all the operants to `f64`:
let (m, v, p) = (self.m.cast::<f64>(), self.v.cast::<f64>(), self.p.cast::<f64>());
// Perform the computation with f64 precision, then
// cast the result to f32.
(p + m * v * dt as f64).cast()
}
}
See all the DefaultAllocator: Allocator<...> trait bounds? They are here to help the compiler
deduce the proper storage types for the matrix/vector/points (i.e. to deduce the GenericArray
with the right dimensions).
Now that const-generics have been integrated to nalgebra this code becomes as simple as one would expect:
use nalgebra::{Point, SMatrix, SVector};
struct Integrator<const D: usize> {
m: SMatrix<f32, D, D>,
v: SVector<f32, D>,
p: Point<f32, D>,
}
impl<const D: usize> Integrator<D> {
// A method that performs some kind of integration
// using `f64` intermediate results.
fn integrate_highp(&self, dt: f32) -> Point<f32, D> {
// First cast all the operants to `f64`:
let (m, v, p) = (
self.m.cast::<f64>(),
self.v.cast::<f64>(),
self.p.cast::<f64>(),
);
// Perform the computation with f64 precision, then
// cast the result to f32.
(p + m * v * dt as f64).cast()
}
}
See that there isn't any DefaultAllocator: Allocator trait bounds whatsoever.
Now, keep in mind that these simplifications will only work if you stick with entities
with dimensions known at compile-time. If your code needs to work generically for both
statically-sized matrices and dynamically-sized matrices, then the DefaultAllocator: Allocator
bounds are still necessary (we should be able to get rid of them too once specialization
is stabilized).
2. Simpler debugging of small matrices and vectors
This one is a life-changer for those relying extensively on debuggers. Until now,
inspecting with a debugger the content of statically-sized matrices or vectors (or
points, quaternions, etc.) was extremely difficult. This was caused by the smart,
but complicated, recursive definition of GenericArray. Here is what inspecting
the content of let matrix = Matrix2::new(1, 2, 3, 4) looked like (in CLion's debugger,
using the Rust plugin):
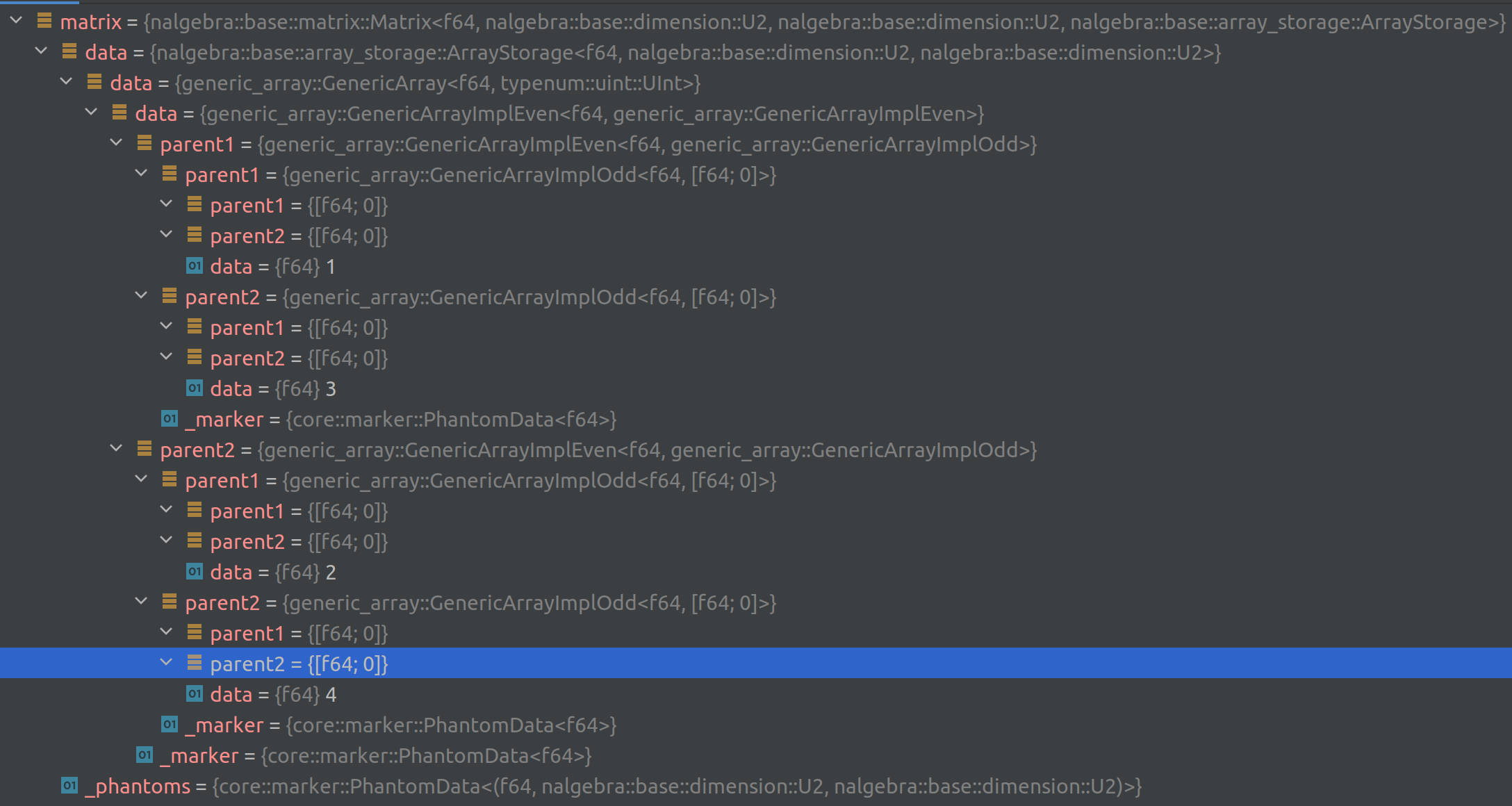
Here is what it looks like now that we replaced GenericArray by standard arrays:

This is much clearer now. Keep in mind that nalgebra stores its matrices in
column-major format. That's why the components appear in the order [[1, 3], [2, 4]] (column
by column).
3. Building small, constant, matrices and vectors
Now that small matrices are using standard arrays under the hood, it is now possible
to define constant vectors, matrices, points, quaternions, and translations by using
their const fn new(...) constructors:
use nalgebra::{Vector3, Point4, Matrix2, Quaternion, Translation3};
const VECTOR: Vector3<u32> = Vector3::new(1, 2, 3);
const POINT: Point4<f32> = Point4::new(1.0, 2.0, 3.0, 4.0);
const MATRIX: Matrix2<i32> = Matrix2::new(-1, 2,
-3, 4);
const QUATERNION: Quaternion<f64> = Quaternion::new(1.0, 2.0, 3.0, 4.0);
const TRANSLATION: Translation3<f32> = Translation3::new(1.0, 2.0, 3.0);
4. New aliases
Everything in nalgebra ends up being expressed as a matrix, in one way or another. Even
a vector is just the Matrix type setup to have only one column. This is why we have so many
type aliasses like Vector3 which is an alias for a matrix with 3 rows and one column.
In nalgebra 0.26 we have the following dimension-generic type aliases:
OMatrix<T, R: Dim, C: Dim>: for owned matrices (formerly calledMatrixMN), i.e., matrices that own their components (as opposed to matrix slices that borrow them).SMatrix<T, const R: usize, const C: usize>: for statically-allocated matrices.DMatrix<T>: for dynamically-allocated matrices.
All the aliases for specific dimensions (e.g. Vector3 for 3D vectors) remain unchanged.
The same applies to vectors: OVector, SVector, DVector. For example a statically-sized vector
with 528 components can be written SVector<f32, 528>.
Limitations: why typenum is still needed
We no longer use the generic-array crate, but you will notice that nalgebra continues
to depend on the typenum crate. This is needed because const-generics support on Rust 1.51
isn't complete yet, and doesn't allow operations on the const-parameters like in the following
push method that adds an element to an array:
impl<T, const LENGTH: usize> Vector<T, LENGTH> {
// The { LENGTH + 1 } isn't allowed yet in this context.
fn push(self) -> Vector<T, { LENGTH + 1 }>
{ unimplemented!() }
}
In order to overcome this limitation, we have to rely on typenum by converting the
integer to a type-level-integer, performing the operation with typenum's type-level operators,
and then extracting the result as a const value. This roughly looks like this:
struct Const<const D: usize>;
trait ToTypenum {
type Output;
}
trait ToConst {
type Output;
}
impl ToTypenum for Const<1> { type Output = typenum::U1; }
impl ToConst for typenum::U1 { type Output = Const<1>; }
impl ToTypenum for Const<2> { type Output = typenum::U2; }
impl ToConst for typenum::U2 { type Output = Const<2>; }
// ... make the same impl. for all values until some arbitrary
// limit (currently 127 in nalgebra).
impl<const R: usize> Vector<N, Const<R>> {
fn push(&self) -> Vector<N, <Sum<<Const<R> as ToTypenum>::Output, typenum::U1> as ToConst>::Output>
where Const<R>: ToTypenum,
<Const<R> as ToTypenum>::Output: Add<typenum::U1>,
Sum<<Const<R> as ToTypenum>::Output, typenum::U1>: ToConst {
unimplemented!()
}
}
It's actually less verbose in nalgebra because we have some additional traits to hide some
of the complexity going on here. But the fact remains that without more advanced const-generics
support from the compiler, methods like this push will be more verbose to define, and will be limited
to the values of D (currently the values in [0, 127]) such that Const<D>: TyTypenum is implemented.
What's next?
The const-generics MVP allowed us to significantly improve the ergonomics of statically-sized matrices and vectors. However, we are still waiting for two features to land to make nalgebra much nicer:
- Specialization: with specialization in place, we could get rid of all the
DefaultAllocator: Allocator<...>bounds. This means writing generic code that accepts both statically-sized matrices and dynamically-sized matrices would become much easier. - Const-generics (the complete version): being able to write something like
[T; { LENGTH + 1 }]would allow us to remove thetypenumdependency completely. - Const-fn (the complete version): being able to have trait bounds other than
Sizedin generic const-functions would allow us to mark most of nalgebra's methods asconst. Right now, only some constructors are possible.